基于新型激光场结构的光场调控是当前光学与光子学领域的重要研究方向。光场调控主要分为线性调控（如调控色散和衍射、角动量、自旋轨道耦合）和非线性调控（调控介质的非线性特性，如非线性光子晶体）两种手段。在量子多体物理和凝聚态物理领域，如物质的第五态玻色-爱因斯坦凝聚态（前四种物质为固体、液体、气体和等离子体）也存在类似的调控方法，谓之量子调控——其中实验科学家最广为采用的两种方法是光晶格（线性调控）和费希巴赫共振（非线性调控）。 

　　玻色-爱因斯坦凝聚（更广泛地说，冷原子）是一种天然的非线性物质，因为其内部原子-原子之间的相互碰撞会产生非线性效应；为此，玻色-爱因斯坦凝聚中涌现出诸多非线性现象，比如物质波的四波混频、亮孤子和暗孤子、涡旋与涡旋晶格、动态不稳定性等等。除了在基础科学研究的重要作用，玻色-爱因斯坦凝聚在实际应用中还具有广阔的前景，比如用作冷原子干涉仪、原子激光器、具有前所未有精度的冷原子钟和精密测量技术，以及更令人兴奋的量子信息处理领域。 

　　近期，中国科学院西安光机所瞬态光学与光子技术国家重点实验室阿秒科学技术研究方向曾健华副研究员团队在前沿光子学的线性和非线性调控理论研究方面取得系列重要进展，研究成果发表在《Advanced Photonics》、《Optics Letters》、《Journal of the Optical Society of America B》等光学期刊上。 

　　2019年8月27日，题目为《囚禁于光晶格帯隙中的玻色-爱因斯坦凝聚暗局域模》（Gap-type dark localized modes in a Bose–Einstein condensate with optical lattices）的理论研究工作发表在光学期刊《Advanced Photonics》（https://doi.org/10.1117/1.AP.1.4.046004）。将冷原子束缚于光晶格中为研究各种有趣的物理特性和丰富的非线性动力学现象提供了一个干净的、易于实现和精确控制的实验平台，这与固体物理中的晶体相比具有显著的优势。光晶格作为易实现和易操作的多功能手段，存在类似于半导体材料中的能带结构，在探索玻色-爱因斯坦凝聚特性和操控其动力学方面具有得天独厚的优势，一个标志性成果就是在实验中用光晶格实现亮的物质波带隙孤子。然而，暗的带隙孤子仍未在实验中观测到，其在高维度的物理特性仍然悬而未决。发表在《Advanced Photonics》的工作通过严格的理论和数值模拟方法，研究了囚禁于一维和二维光晶格带隙中的冷原子暗局域模的产生和稳定特性，发现了两类稳定的暗局域模，即暗的带隙孤子和带隙孤子簇；同时，研究了在二维结构中这两类暗局域模所对应的涡旋态。研究工作为在冷原子和光学（使用光子晶体和光学晶格）前沿实验中观测暗的局域带隙波结构开辟了新的途径。鉴于该工作的创新性和重要性，论文发表当天就被SPIE（国际光学工程学会）主页选为“Highlighted stories”（亮点故事，网址： https://spie.org/news?SSO=1）并加以宣传介绍（网址：https://spie.org/news/stabilizing-2-d-dark-gap-solitons-and-vortices-using-bright-defects-in-optical-lattices）。

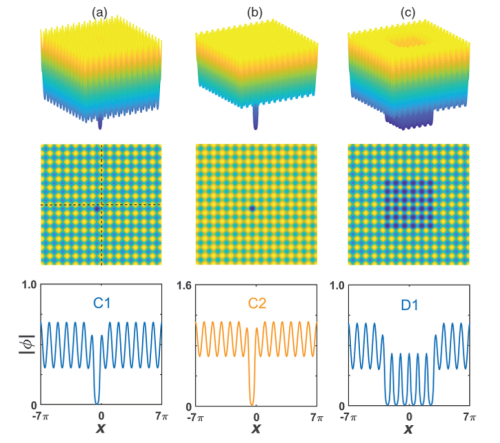
　　　　图1. 二维空间中的帯隙型暗孤子与暗孤子簇的三维结构图（上行）、俯视图（中行）及其波形（下行）：位于第一（a）和第二（b）带隙中的暗孤子；（c）暗孤子簇。[ Advanced Photonics 1, 046004 (2019)] 

　　  该团队在非线性孤子理论方面也取得系列重要结果，如题目为《纯克尔非线性模型/介质中的平顶孤子》（Purely Kerr nonlinear model admitting flat-top solitons）的理论研究工作发表在《Optics Letters》（https://doi.org/10.1364/OL.44.001206）。文章首次借助纯非线性调控方法预测了一类新型的孤子结构，并通过解析和数值计算两种方法研究了平顶孤子和非线性激发模(多级偶极子和涡旋)结构的存在条件和稳定性情况。 

　　　图2. 纯非线性调控下的一维平顶孤子。基模（a）；偶极（b）和三极（c）激发模。红线为非线性势阱形状。[ Optics Letters 44, 001206(2019)]  

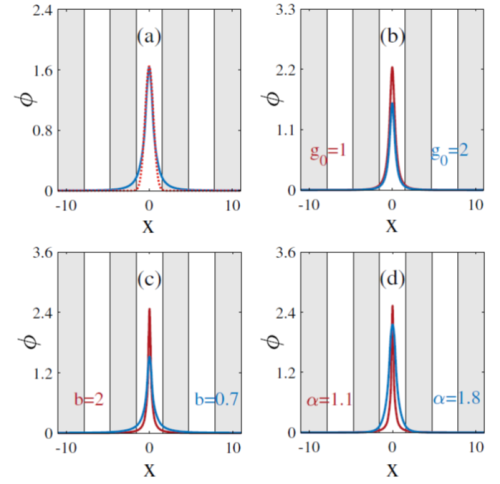
　　图3. 分数衍射调控和非线性晶格调控下的一维孤子结构。（a）基模与高斯光（虚线）的波形对比；在不同非线性强度（b）、传播常数（c）和衍射阶数（d）下的激光波形变化情况。[ Optics Letters 44, 002661 (2019)] 

 

　　2019年5月17日，题目为《具有空间周期性调制非线性（非线性晶格）的分数薛定谔方程中的一维孤子》（One-dimensional solitons in fractional Schr？dinger equation with a spatially periodical modulated nonlinearity: nonlinear lattice）的理论研究工作再度发表在《Optics Letters》（https://doi.org/10.1364/OL.44.002661）。文章首次结合非线性调控方法和线性衍射调控方法，通过严格的理论分析和数值实验，研究了多种一维孤子结构（基态模和激发模）的产生条件和在各种调制物理参数情况下的稳定特性。此外，题目为“具有空间调制排斥非线性作用的超冷原子中的类高斯和平顶孤子”（Gaussian-like and flat-top solitons of atoms with spatially modulated repulsive interactions）的理论研究工作于2019年7月29日发表在《Journal of the Optical Society of America B》（https://doi.org/10.1364/JOSAB.36.002278）。 

　　

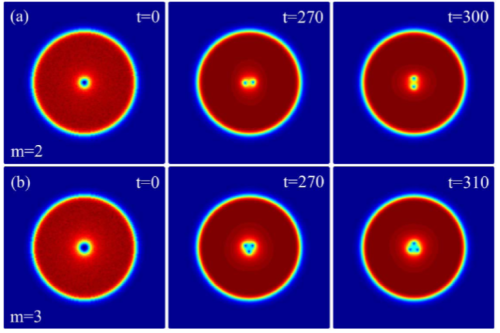
　　图4. 在空间调制排斥非线性超冷原子中的平顶涡旋波结构的动力学演化。在角动量守恒条件下，涡度为2（第一行）和3（第二行）的涡旋波结构分别演化成2个和3个旋转的单涡旋。[ J. Opt. Soc. Am. B 36, 002278 (2019)] 

　　以上工作是西安光机所曾健华副研究员（中国科学院青促会会员）及其研究生团队完成，第一作者为博士生曾亮维。曾健华老师系中山大学和以色列魏茨曼科学研究所联合培养光学博士，曾在以色列特拉维夫大学和清华大学物理系从事博士后研究工作；2013年8月起加入西安光机所瞬态光学与光子技术国家重点实验室任副研究员，2015年被评为博士生导师。 

 

 以上研究工作也得到国家自然科学基金和中国科学院青年创新促进会的支持。（瞬态室  供稿）